Circles and its Related Terms

Find the length of the chord $AC$ where $AB$ and $CD$ are the two diameters perpendicular to each other of a circle with radius $4\sqrt{2} \mathrm{cm}$ and also find $\angle OAC$ and $\angle OCA$.

A region bounded by two radii and an arc is called

A straight line which intersects the circle at two points is called

Write the exterior points of the following circle

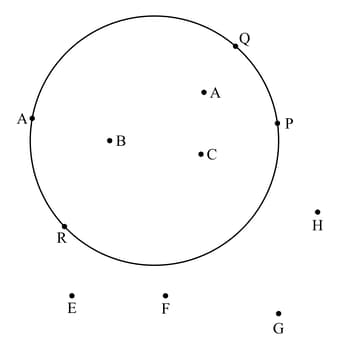
Write the exterior points of the following circle

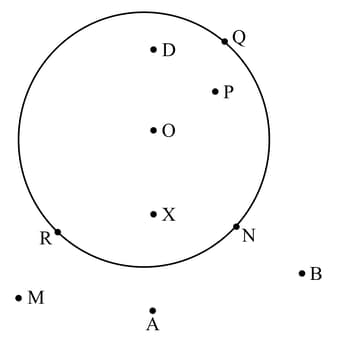
A chord of a circle of radius $10 \mathrm{cm}$ subtends a right angle at the centre. Find the area of the major sector.

Find the area of the sector of a circle with radius $2 \mathrm{cm}$ and an angle of $20°$. Also, find the area of the corresponding major sector. (Use $\mathrm{\pi }=3.14$)

Find the area of the sector of a circle with radius $4 \mathrm{cm}$ and of angle $30°$. Also, find the area of the corresponding major sector. (Use $\mathrm{\pi }=3.14)$

A line segment connecting the centre of a circle to any point on the circle itself is called

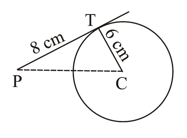
In the adjoining figure, $C$ is the centre of the circle. The tangent to the circle of radius $6 \mathrm{cm}$ from a point $P$ outside the circle is of length $8 \mathrm{cm}$. If the distance of the point $P$ from the farthest point of the circumference is $k \mathrm{cm}$, then find the value of $k$.

The area of the circle, whose radius is $4.2 \mathrm{cm}$ is

The circumference of the circle, whose radius is $17.5 \mathrm{cm}$ is

Angle formed in minor segment of a circle is

Sector is the region between the chord and its corresponding arc.

If a circle is divided into three equal arcs each is a major arc.

Segment of a circle is the region between an arc and _____ of the circle.

A continuous piece of a circle is _____ of the circle.

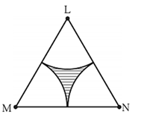
$\mathrm{\Delta LMN}$ is an equilateral triangle. $\mathrm{LM}=14 \mathrm{cm}$. As shown in figure, three sectors are drawn with vertices as centres and radius $7 \mathrm{cm}$. Find, $\mathrm{A}(∆\mathrm{LMN})$ in centimetres correct upto two decimal places.

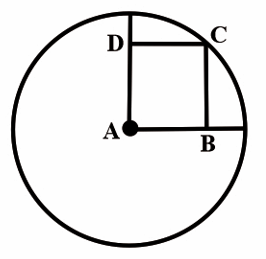
$A$ is the centre of the circle and $ABCD$ is a square. If $BD=4 \mathrm{cm}$ then find the radius of the circle in $\mathrm{cm}$.

The tangent at any point of a circle and the radius through that point are _____ to each other.